Les nombres dans la Bible (introduction)

• Des nombres et des symboles :

Sur le sujet immense de l’utilisation, dans la Bible, du symbolisme numérique, une brève introduction est indispensable. D’autant que les affirmations les plus contradictoires abondent. 

S’il est un sujet mal connu, c’est bien celui-là. On est « pour » ou l’on est « contre ». A priori. D’un côté, nous trouvons des considérations apologétiques -parfois délirantes- sur ces nombres mystérieux qui « prouvent » ceci ou cela et, d’un autre côté, des études sérieuses qui ignorent superbement la dimension symbolique attachée à la mise en forme de nombreux textes bibliques.

Il est vrai que la question est complexe et, souvent, cette démarche est étrangère à nos modes de pensée. Il n’y a donc pas d’échappatoire : il faut expliquer les fondement d’un langage qui est –en soi- simple, mais dont les présupposés nous sont peu familiers. Il faut ensuite n’exposer que des faits contrôlables. Toute affirmation doit être étayée par une ou plusieurs références dans les textes bibliques.  Libre à chacun de tirer telle ou telle conclusion de l’observation. Le cas cependant n’est pas rare de conclusions fausses tirées d’observations justes. Prudence s’impose donc !

Pour autant, négliger cette étude revient à se couper d’informations importantes sur la manière dont les scribes anciens ont donné aux textes bibliques (Bible hébraïque et Nouveau Testament grec, mais aussi écrits dits « apocryphes », juifs ou chrétiens) une forme qu’ils jugeaient significative.

La compréhension du symbolisme des nombres et l’étude de son utilisation dans les textes est un domaine souvent méconnu, mais cependant bien digne d’étude. Naturellement, les observations qui suivent (et suivront) ont déjà fait l’objet de publications et –donc- d’examen critique. Elles sont aujourd’hui le bien de tous.

Dans tous les cas, l’accès à ce langage symbolique suppose une initiation à d’anciennes méthodes de calcul. C’est le propos des lignes qui suivent. Elles sont un préalable à la compréhension des chiffres utilisés dans la Bible (surtout dans des écrits tardifs –psaumes et apocalypses).

•  Au commencement était Pythagore…   

Dès le début, il importe de se faire une représentation juste de l’appréhension des nombres dans la pensée des anciens. De ce point de vue, l’ancien pythagorisme et les commencements de l’arithmétique sont éclairants. Et il ne s’agit pas de deux mondes séparés : le pythagorisme et le monde biblique. Il faut se souvenir que dès l’empire perse (et donc avant les conquêtes d’Alexandre et l’hellénisation du Proche-Orient), les connaissances grecques sont diffusées dans cette partie méditerranéenne.

Ionie, Syrie, Palestine sont alors liées, non seulement par un empire perse commun, mais aussi par des courants d’échange (marchands, mercenaires, voyageurs…). Des enseignements de l’ancienne école pythagoricienne (début 5^ème siècle avant notre ère) sont diffusées non, certes, dans un grand public, mais dans quelques cercles savants. Cela est vrai pour les milieux où la Bible est mise en forme, à la même époque.

Evidemment, les présupposés religieux sont différents. Cependant, l’opposition juive à la pensée hellénistique ne viendra que beaucoup plus tard. Les cercles intellectuels (même religieux) ignorent alors cette rupture. Et jusqu’aux victoires d’Alexandre (dans la deuxième moitié du quatrième siècle avant notre ère) l’Ionie est une satrapie de l’empire perse, comme la Transeuphratène (dont la Judée est une petite partie) .

L’arithmétique naissante est emplie de considérations religieuses. Arithmétique géométrique dans laquelle les nombres sont des formes et toute forme a un nombre. Ce sont là des évidences « scientifiques », à cette époque, et elles sont indépendantes de tout a priori confessionnel. D’ailleurs, tout est nombre et –dans une perspective juive- tout ce qui existe procède du seul Dieu créateur. Lois physiques et lois religieuses appartiennent au même ordre du monde. Pour tous, les nombres sont le miroir de cette harmonie.

Science et religion ne sont pas séparées. De fait, la séparation ne viendra, très lentement (et très inégalement selon les lieux et les cultures) que bien des siècles plus tard. A l’époque biblique, une telle séparation n’existe pas.

• Des cailloux…   

Pour faire bref, rappelons que l’on compte alors, normalement, avec des cailloux. Nous avons conservé le souvenir de cela dans le vocabulaire de la médecine : avoir des « calculs » dans les reins ou dans la vessie, signifie avoir des cailloux ! Calculer (latin : calculare) se fait avec des calculi –des cailloux. Même association en grec (psêphos est un caillou et psêphidzô signifie « je compte »).

Les cailloux permettent de figurer un nombre. Un caillou figure un point ; deux cailloux figurent une ligne ; trois cailloux figurent un triangle ; quatre cailloux un carré etc… On parle parfois de nombres figurés ou « nombres-polygones » lorsque ces figures s’inscrivent  dans un cercle. Les quatre premiers nombres donneront l’image (triangulaire) de la fameuse « tétraktys » pythagoricienne :

1 + 2 + 3 + 4 = 10 (et donc retour à l’unité dans la numération décimale des grecs (non pour les sémites, chez qui la base de numération est 60). On dira que le nombre triangulaire de 4 est 10 ou encore que la racine triangulaire de 10 est 4.

Mais notre propos n’est pas de nous arrêter sur cette figure très riche de sens. La symbolique biblique est étrangère aux spéculations  sur la tétraktys pythagoricienne. Par contre, les figures formées  (triangle, carré, pentagone) paraissent symboliquement significatives. Arrêtons-nous un peu sur ce point.

On sait que tout nombre appartient à une « famille ». Par exemple, la famille des multiples d’un nombre n ; ou bien la « famille » des carrés… Il en est beaucoup d’autres. Seuls les nombres dits « premiers » ne forment pas une famille. Ils sont un groupe, non une famille. Pourquoi ? C’est qu’ils ne sont pas liés entre eux par un gnomon. Ce gnomon (ce lien de famille) désigne la quantité qui doit être ajoutée au membre d’une « famille » pour obtenir le nombre suivant, au sein de la même famille. Le calcul de ce gnomon est un des plus vieux problèmes que les anciens mathématiciens ont dû résoudre –nous sommes aux balbutiements de l’arithmétique. 

Et d’abord : Pourquoi ce nom « gnomon » qui signifie « équerre » en grec ancien ? Le terme a été imposé par cet usage ancien de déterminer le nombre de cailloux qui s’ajoutent, dans la suite des carrés, grâce à des équerres.

Soit une figure carrée composée de deux lignes de deux cailloux ; trois lignes de trois cailloux ; quatre lignes de quatre cailloux et ainsi de suite…  Puis qu’une équerre soit placée au bord de chaque carré ainsi formé. Il suffira alors de compter le nombre des cailloux entre deux équerres pour connaître le nombre qui permettra de passer d’un carré à l’autre : 

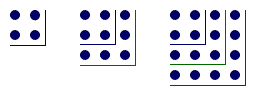
Un moderne utiliserait une écriture algébrique plus rapide (mais non visuelle). Soit un carré n²  : que faudrait-il ajouter pour obtenir le nombre (n + 1)². ? Tout potache saurait aujourd’hui que la formule donne : n² + 2n + 1. Ce qui est ajouté à n² est donc : 2n + 1. C’est ce résultat que le nombre de cailloux entre deux équerres rendait évident : 5, 7, 9, 11 etc…
Soit 2 + 2 + 1 ; 3 + 3 + 1 ; 4 + 4 + 1  etc…

• Des figures   

Cette arithmétique élémentaire sera étendue aux autres figures (triangles, pentagones, hexagones…) dont le gnomon (le lien de famille) sera :
Triangulaires (Tn) :  n + 1
Carrés  (Cn = n²)  :   2n + 1
Pentagonaux (Pn): 3n + 1
Hexagonaux (Hn): 4n + 1
Etc…

Il importe de se familiariser avec ces cailloux, afin de comprendre ce qui suit. C’est à ce prix que peut apparaître la simplicité d’un système bien connu de certains auteurs bibliques. Dès l’enfance, nous connaissons les carrés, mais non toujours les nombres attachés aux autres figures….

Le carré a été appelé ainsi, parce qu’une figure (construite avec des cailloux) était carrée. Ajoutons que tout carré peut être décomposé en deux triangulaires de nombres consécutifs :

T3

T4

T3 + T4 = 6 + 10 = 16 = 4²;

Ce nombre triangulaire précédent (Tn – 1) est un nombre fort important. C’est en effet le gnomon d’une nouvelle famille : celle qui est constituée par la série des nombres-figures (ou nombres polygones), ainsi que le montre le tableau suivant :

Il est donc fort simple de passer de l’un à l’autre des nombres figurés si l’on connaît le gnomon. Il suffit d’ajouter le triangulaire du nombre précédent. Il est inutile d’utiliser des formules plus compliquées qu’un moderne (surtout s’il possède une calculette !) emploierait. Ainsi le pentagonal d’un nombre (Pn) est :

               Pn =  n (3n – 1)
                             2

               P7 = 7 (21 –1) = 70
                             2  

Mais la méthode du gnomon est encore plus simple :

               49 (= C7) + 21 (= T6) = 70

Autrement dit, d’un point de vue de l’exégèse symbolique, 70 (= P7)
et 49 (= C7 ou 7²;) ont la même racine. Ainsi, par exemple, les 70 années d’exil, dans la prophétie de Jérémie, pourront être lues comme se rapportant à un exil qui a historiquement duré 49 ans. Dieu est le maître de l’histoire, comme de la prophétie. Encore faut-il savoir décrypter cette dernière pour comprendre l’autre. C’est ce que fera Daniel (cf Daniel 9,2).

Comme les triangles et les carrés, les pentagones engendrent des figures semblables qui comptent autant de cailloux que de points homothétiques :

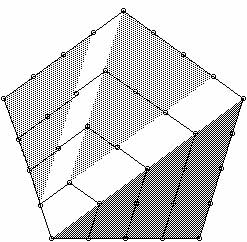
• Rectangulaires (Rn)    

Il faut faire ici une place aux nombres dits « rectangulaires ». Les cailloux sont alors disposés en forme de rectangle. La longueur compte un caillou de plus que la largeur, de sorte que le nombre rectangulaire est de la forme n (n + 1) : 2 x 3 ; 3 x 4 ; 4 x 5 etc…

Un nombre rectangulaire est toujours le double d’un triangulaire. Ce dernier est ainsi :

               Tn = n (n + 1)
                         2

On parlera donc de « racines » triangulaires, rectangulaires, carrées, pentagonales… selon le nombre-source qui est utilisé symboliquement. La « racine » seule est significative. Les nombres n’ont pas, comme pour nous, une simple valeur quantitative, mais surtout une valeur qualitative. C’est ici que l’arithmétique touche à l’exégèse. Dans tout nombre, il importe de connaître cette racine symbolique.

Triangulaires : 28 (= T 7), 36 (= T8) , 91 (= T13) , 153 (= T17) , 666 (= T36)
Rectangulaires : 12 (= R3), 42 (= R6) ,
Carrés : 36 (= C6) , 49 (= C7) , 144 (= C12) , 361 (= C19) ,
Pentagonaux : 35 (= P5) , 7O (= P7) , 276 (= P12) , 1001 (= P26) , 1335 (= P30) ,

• S’arrêter aux pentagonaux    

Nous pouvons laisser de côté, ici, les nombres hexagonaux. Non qu’ils n’aient pas de fonction, ni qu’ils soient difficiles à calculer puisqu’une simple addition suffit (Hn = Pn + Tn-1). Un moderne calculateur préfèrera sans doute : Hn = n (2n – 1). De fait, Hn et les nombres figurés suivants sont bien connus des anciens.

Boèce –suivant en cela l’enseignement du néo-pythagoricien Nicomaque de Gérase et de l’école d’Alexandrie-  montre comment calculer ces nombres figurés (cf Boèce : Institution arithmétique, Paris 1995 –texte latin et traduction française par J-Y. Guillaumin).

Mais il y a une autre raison de s’arrêter aux nombres pentagonaux. D’un point de vue symbolique, 5 est une culmination. Pensons aux cinq corps platoniciens, dont le dernier (le dodécaèdre :12 faces qui sont des pentagones) figure l’éther qui enveloppe tout ce qui existe. Jusqu’à Kepler, cette conception sera régnante.

Pour les pythagoriciens, l’étoile à 5 branches était le signe des disciples. Si tout ce qui existe –dans ce monde sublunaire- est analogue au point, à la ligne, à la surface ou au volume (et donc tout est figuré par la tétraktys = T4), le nombre 5 doit référer à ce qui pointe au-delà de ce monde.

Et ce sera dans la Bible une partie (1/5 ou O,5 ou 5… selon les contextes) de la totalité figurée par la base de numération 60 (5 x 12 = 60). De là, la Thora (le Pentateuque) appelée : « les cinq cinquième de la Loi » ; les 5 « rouleaux » ; les cinq parties du livre des psaumes…Mais, également, la « part » fixée pour un prélèvement, une amende, une taxe (cf Lévitique 27, par exemple). 

• Autres nombres   

Certains nombres posent un problème particulier et doivent donc être interprétés dans le(s) contexte(s) où ils sont employés. C’est évident pour le nombre 5. Sa graphie hébraïque a d’ailleurs suscité bien des commentaires… La littérature exégétique traditionnelle garde parfois les traces d’un enseignement beaucoup plus ancien que la date de rédaction des textes connus.

Il arrive aussi qu’un nombre soit de la forme n²; + 1 ou n²; - 1.. Les années du jubilé sont 5O. Soit : 7²; + 1. Après 7 semaines d’années, 1 commence un nouveau cycle.

Un exemple de nombre de la forme n²; - 1. Les hommes de David tuent 360 guerriers (II Samuel 2,30), tout en ne perdant que 19 hommes. Or 19²; = 361. Ce carré –1 est, certes, une manière d’exprimer la victoire écrasante des gens de David, mais non une extermination qui n’aurait pas laissé de place à une future réconciliation (laquelle aura lieu, selon II Samuel 3,12).

D’autres nombres encore jouent un rôle dans un contexte particulier. Ainsi, une proportion 2/3 revient régulièrement.. C’est le cas de 40/60. Le nombre 40 signifie un temps d’épreuve suivi du passage à un stade différent. Les exemples sont nombreux (40 ans dans le désert, 40 jours de tentation, 40 jours de répit avant le bouleversement de Ninive…).

Ce qu’on nomme « proportion dorée » est également important dans les constructions bibliques. Evidemment, dans le langage particulier à cette époque –et sans faire intervenir des calculs connus beaucoup plus tard.  Les nombres irrationnels sont remplacés par approximation fractionnaire. De toutes façons, c’est ici un rapport entre DEUX nombres (3/5 ou 30/50 ou 1,5 / 2,5). Inutile donc, dans ce cas, de chercher à  interpréter séparément un seul de ces nombres.

Une difficulté de cette étude est qu’un système unique n’existe pas. Bien des tentatives d’interprétation ont échoué en voulant « découvrir » un système unique. Il faut au contraire –dans chaque contexte particulier- examiner la symbolique qui est mise en œuvre. Les nombres figurés jouent un rôle important, mais tel nombre peut référer à une autre base symbolique.

Les guématries (valeurs numériques des lettres d’un mot) sont une utilisation particulière qui connaîtra de grands développements hors de la Bible (dans le targum, le midrash et –naturellement- dans la littérature cabalistique). Cependant -malgré ce qu’on dit souvent- ce procédé est connu dans plusieurs textes bibliques. Encore une réalité irréfutable et méconnue… 

Contrairement à ce que l’on écrit encore, parfois, les valeurs numériques des lettres hébraïques sont connues dans l’usage religieux, bien avant d’être utilisées dans l’usage profane. La démonstration ne peut être faite ici, mais les exemples bibliques sont assez nombreux pour que le contraire soit insoutenable.

• Des lettres et des chiffres   

Auparavant, dans le monde hellénisé, les lettres grecques étaient utilisées pour noter les nombres (dès le quatrième siècle avant notre ère) et les hébreux utilisaient, pour l’usage courant, la notation araméenne des marchands. Mais une notation religieuse juive attribue anciennement des valeurs numériques aux lettres de la langue sacrée. 

Cette notation des chiffres au moyen de lettres avait, certes,  l’inconvénient de ne connaître ni zéro, ni écriture de position. Mais dans un usage symbolique, ces inconvénients disparaissaient. D’autant que les nombres figurés fournissaient une représentation visuelle du nombre.

Dans tous les cas, on ne peut séparer une utilisation symbolique des nombres et l’usage courant des nombres au sein d’une culture déterminée. Une appréhension moderne, purement quantitative, du nombre est très éloignée de l’appréhension ancienne (et qualitative) de tel nombre. Une « suite infinie » de nombres abstraits est une notion étrangère aux anciens. Simplement, celui qui compte donne la mesure de ce qui est compté.

« Aux yeux de Dieu, mille ans sont comme un jour », dit le psalmiste (Psaume 90,4 ; cp Psaume 84,11). Mille ans sont une durée quasi éternelle pour l’homme éphémère ! Mais le tétragramme divin a pour valeur numérique : 26. Et le nombre pentagonal de 26 est 1001. Ce 1 désigne ici le commencement d’un nouveau cycle. C’est au bout de mille ans de règne que commencera un monde nouveau, selon l’Apocalypse (cf Apocalypse 20,2 et versets suivants; cp II Pierre 3,8).

Ce même nombre 26 est encore racine symbolique dans un texte pseudépigraphe (La vision d’Esdras) où la flamme qui émane de Dieu mesure 702 pieds. Les justes traversent cette flamme sans être atteints ! Or ce nombre 702 est le rectangulaire de 26 :

R26 = 26 x 27 = 702  (1)

Cela pose le problème de savoir dans quels milieux (juifs et chrétiens) ces computs étaient jugés signifiants. Mais la question est de tous les temps : Comprends-tu ce que tu lis ?

Jacques Chopineau, Genappe le 24 juillet 2003

Note
(1) Nous avions signalé cette utilisation du rectangulaire de 26 dans Analecta Bruxellensia 5 (2000) p 68. Mais d’autres écrits chrétiens d’origine juive témoignent de la permanence d’une tradition symbolique qui trouve sa source dans la Bible ancienne. Le césaro-papisme mettra fin à la diversité des groupes chrétiens primitifs et à leurs lectures. ….